Beyond Experimentation

 

POLSCI 4SS3
Winter 2024

Last two weeks

• Field experiments as the gold standard to evaluate policy

• Many choices in research design and implementation

• Today: How do we learn from experiments?

Learning from experiments

• How do you prove that a policy intervention works?

. . .

• We want to make statements about causation

  • TUP program improves income

. . .

• To back up those statements, we need to rule out confounding factors

  • Those who join the TUP program are more likely to seek economic opportunities

Ruling out confounders

• One way to rule out potential confounders is to conduct an experiment or analyze existing data that looks like an experiment (coming soon!)

. . .

• Challenge: This is only true in expectation

A small experiment

ID	Female	Y(0)	Y(1)
1	0	0	0
2	0	0	1
3	1	0	1
4	1	1	1

. . .

• \(Y(*)\) are the potential outcomes under control (0) and treatment (1), respectively

• \(Y(*) = 1\) means person’s life improves, \(Y(*) = 0\) means life stays the same

A small experiment

ID	Female	Y(0)	Y(1)
1	0	0	0
2	0	0	1
3	1	0	1
4	1	1	1

• We have:

  • One person for which the policy would do nothing
  • Two people for which the policy improves life
  • One person who improves their life either way

Assign policy treatment at random

ID	Female	Y(0)	Y(1)	Z
1	0	0	0	0
2	0	0	1	0
3	1	0	1	1
4	1	1	1	1

. . .

• We happened to randomly assign the policy to the two women

• We only observe the potential outcomes that corresponds to the treatment status

Revealing outcomes

ID	Female	Y(0)	Y(1)	Z	Y obs
1	0	0	0	0	0
2	0	0	1	0	0
3	1	0	1	1	1
4	1	1	1	1	1

. . .

• The true treatment effect is

\[ATE = E[Y(1)] - E[Y(0)] = 3/4 - 1/4 = 1/2\]

• Which we cannot observe in the real world

Revealing outcomes

ID	Female	Y(0)	Y(1)	Z	Y obs
1	0	0	0	0	0
2	0	0	1	0	0
3	1	0	1	1	1
4	1	1	1	1	1

• We can approximate the ATE with \(\widehat{ATE} = 2/2 - 0/2 = 1\)

• We are off the mark! What happens if we redo the experiment?

Redoing the experiment

ID	Female	Y(0)	Y(1)	Z	Y obs
1	0	0	0	1	0
2	0	0	1	0	0
3	1	0	1	1	1
4	1	1	1	0	1

. . .

• We still have \(ATE = 1/2\)

• But now \(\widehat{ATE} = 1/2 - 1/2 = 0\)

• Off the mark in the opposite direction

Why does this happen?

				Experiment 1		Experiment 2
ID	Female	Y(0)	Y(1)	Z	Y obs	Z	Y obs
1	0	0	0	0	0	1	0
2	0	0	1	0	0	0	0
3	1	0	1	1	1	1	1
4	1	1	1	1	1	0	1

. . .

• Perhaps men and women react to the policy differently

• We want to rule out results depending on whether we assign treatments to men or women

Why does this happen?

• Experiment 1: 2/2 women in treatment and 0/2 in control (imbalanced)

• Experiment 2: 1/2 woman in treatment and 1/2 in control (balanced)

. . .

• Does that mean that experiment 2 is free from random confounding?

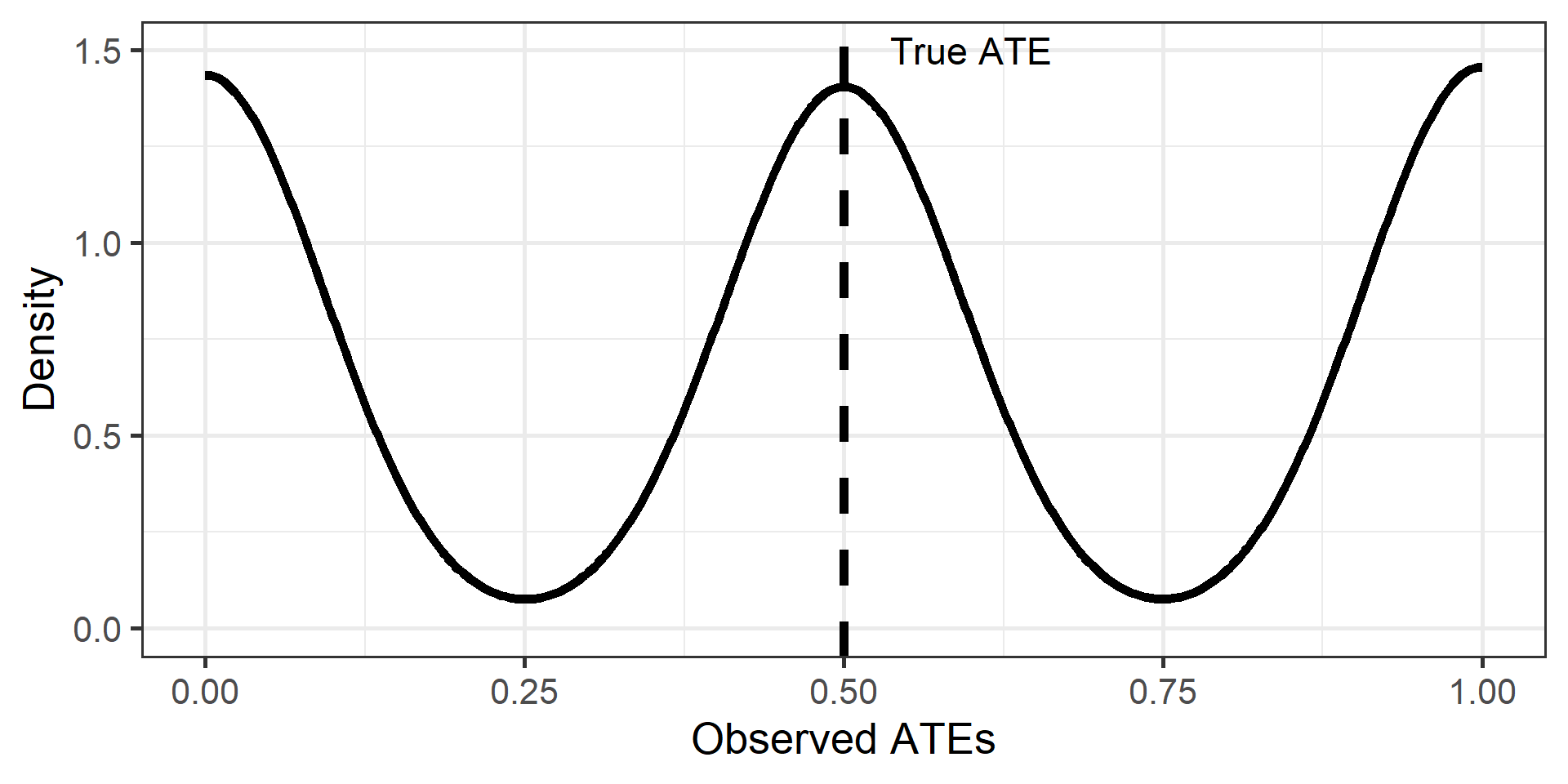
Redo 1,000 experiments

Half of the time we are spot on, half of the time we are wrong in either direction

What does this mean?

. . .

• Experiments only rule out the role of potential confounders IN EXPECTATION

• We can sustain this claim in two ways

. . .

1. With a sufficiently large sample (But how large is large enough?)

2. By repeating the same experiment multiple times (Nobody does this)

In practice

• We only know bias, RMSE, and power in our simulations

• Need a lot of domain expertise to attribute ATE to policy

• This involves explaining why it works

• First step toward knowing whether it would work somewhere else

Generalization and extrapolation

• Critique: Experiments invest in internal validity at the expense of external validity

. . .

• Internal validity: We can (probabilistically) attribute effect to policy intervention

• External validity: Whether effect extrapolates or generalizes

. . .

• Extrapolation: Whether it works elsewhere

• Generalization: Whether it works everywhere

Support factors

• Example: A house burns down because the television was left on

• Not all houses with TVs left on burn down, but sometimes they do, perhaps because the wiring was poor

• A support factor is one part of the causal pie

• Causal pie: A set of causes that are jointly but not separately sufficient for a contribution to an effect (INUS causation)

• Analogy: TUP only works if we have good schools

Scales and drills

. . .

• Scaling up: Whether we can apply intervention to broader area

  • Small scale interventions can become unfeasible or cost-prohibitive in a larger scale

  • Some policies only work at a small scale!

Scales and drills

• Drilling down: Can we apply the results of an intervention to individual units?

  • Just because it works on average, it does not mean that everyone will benefit from it

  • May waste money on people for whom the policy does not work

  • This can be unethical

Coordinated trials

. . .

• Multi-site interventions that evaluate (more or less) the same policy

. . .

• Goals:

  1. Establish whether a policy is generally advisable (pooling results)

  2. Understand why things work in some places but not others (support factors)

Slough et al (2021): Community monitoring of common pool resources

. . .

	Excludable
	Yes	No
Rivalrous
Yes	Private Goods	Common Pool Resources
No	Club goods	Public Goods

Types of goods

Slough et al (2021): Community monitoring of common pool resources

	Excludable
	Yes	No
Rivalrous
Yes	Private Goods	Common Pool Resources
No	Club goods	Public Goods

Types of goods

. . .

• Problem: Prone to congestion, overextraction

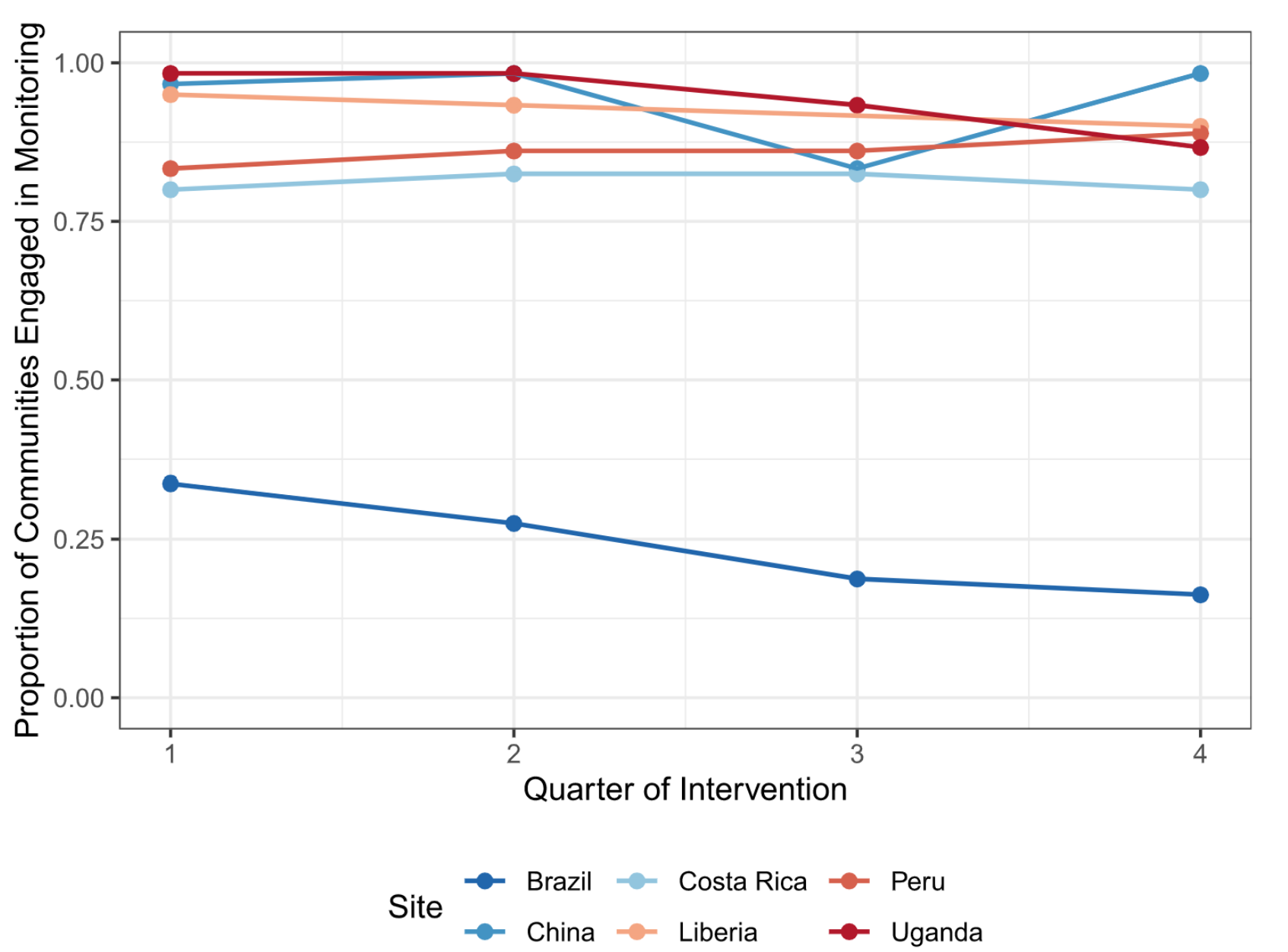
6 different contexts

Country	Resource	Community	Threat
Brazil	Groundwater	Rural villages	Drought, overuse
China	Surface water	Urban neighborhoods	Pollution
Costa Rica	Groundwater	Rural villages	Drought, overuse
Liberia	Forest	Villages	Overcutting
Peru	Forest	Indigenous communities	Extraction
Uganda	Forest	Villages	Overcutting

Interventions

				Dissemination
Country	Wokshops	Training	Monitoring	Citizens	Management
Brazil	X	X	X	X
China		X	X	X
Costa Rica	X	X	X	X	X
Liberia	X	X	X	X	X
Peru	X	X	X	X	X
Uganda	X	X	X	X	X

Findings

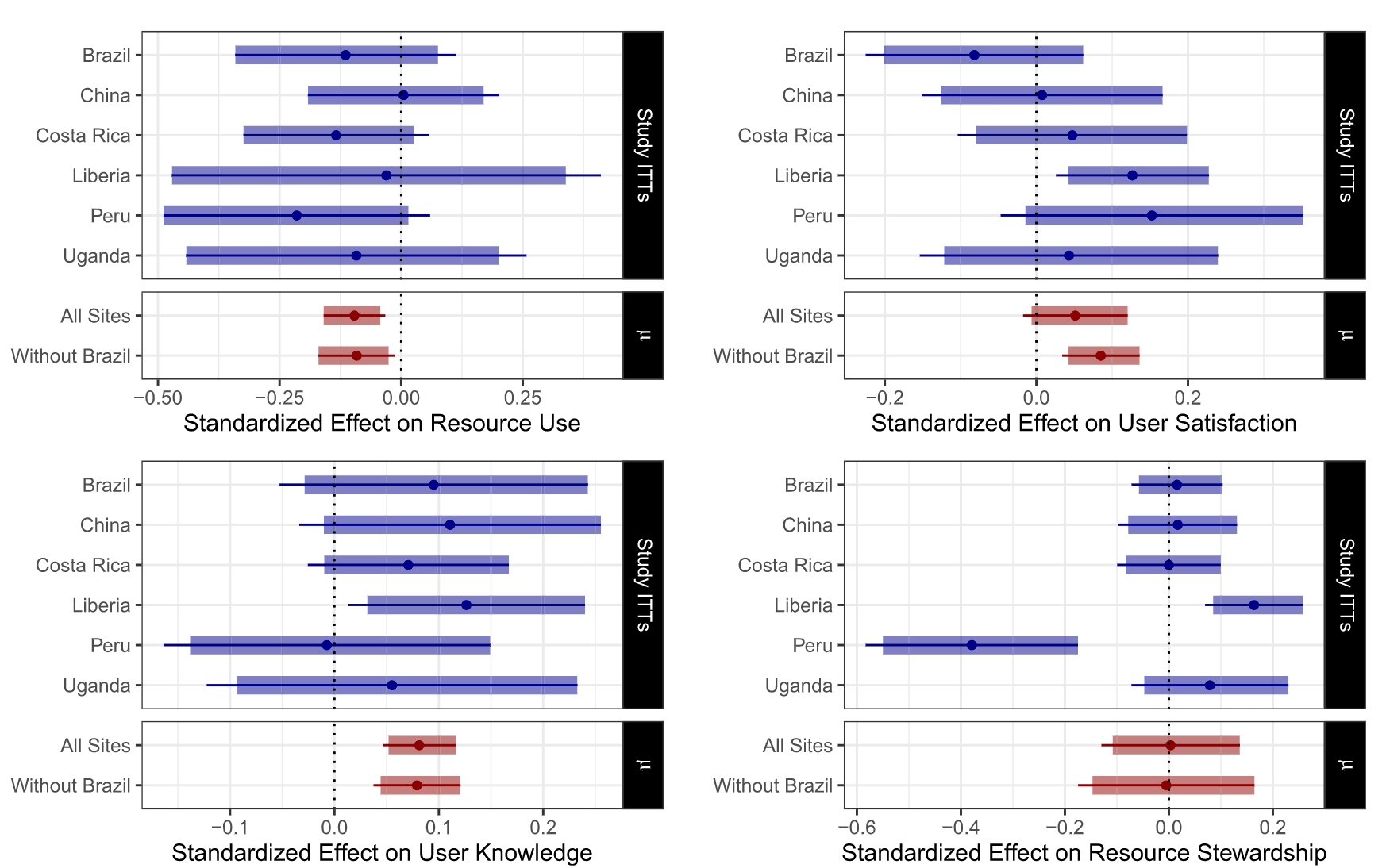
Why without Brazil?

. . .

Next Week

Quasi-experiments

Focus on: What makes these designs credible?

Break time!

 

Lab